Probability Theory - Fall 2022
Overview
Welcome to my course on Probability Theory for third-year students of Bachelor’s Programs “Computer Science”, “Aerospace Engineering” and “Biomedical Engineering” at MIPT.
This is the second part of the course. We will devote this semester to the generalization of the concept of a random variable as a measurable function. We will extensively use the CDF and the PDF of random variables to compute all their interesting numerical characteristics. As a whole, we will completely construct the concept of a propability space . We will conclude our course with the study of some limit theorems.
Problem sets
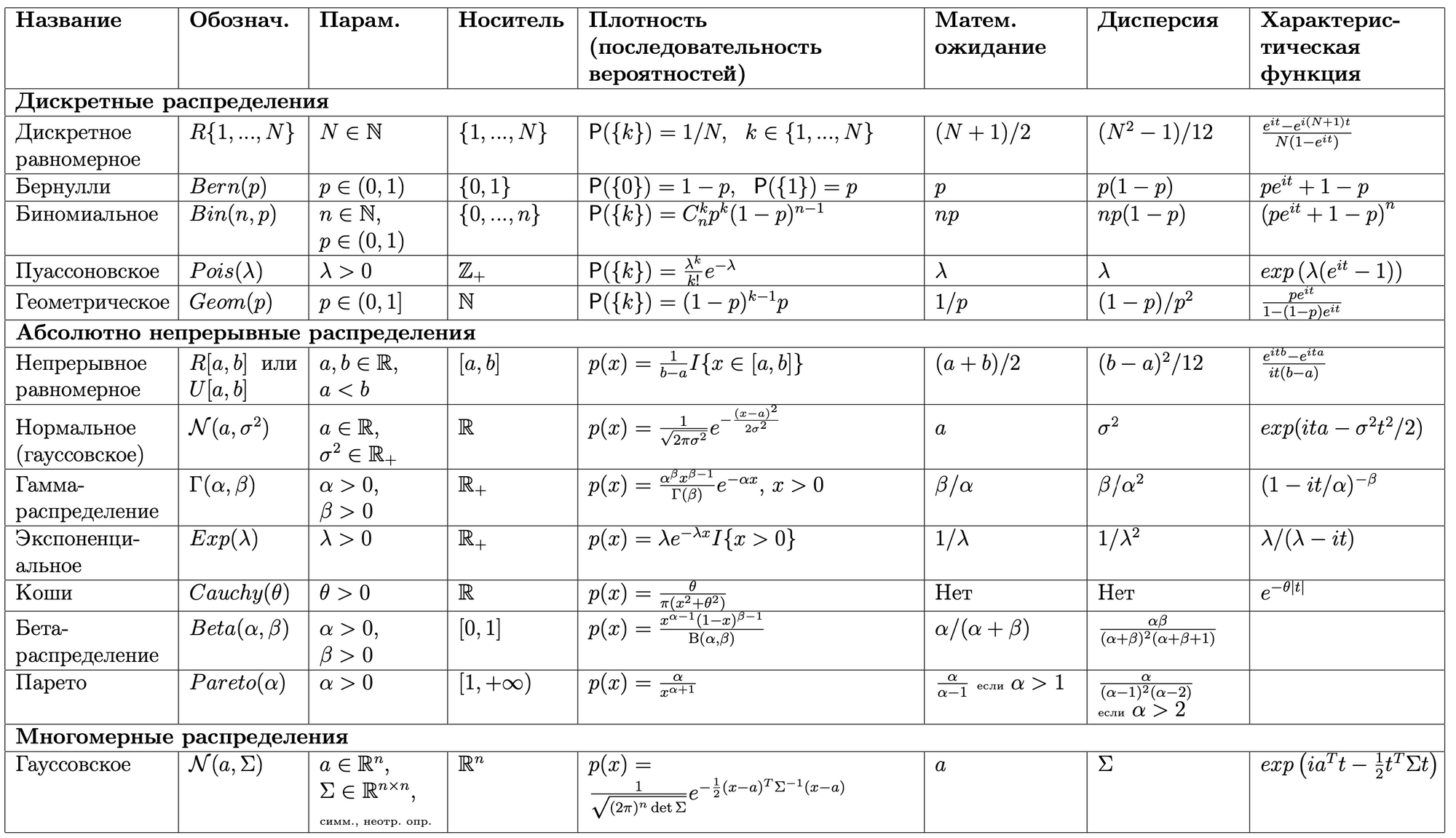
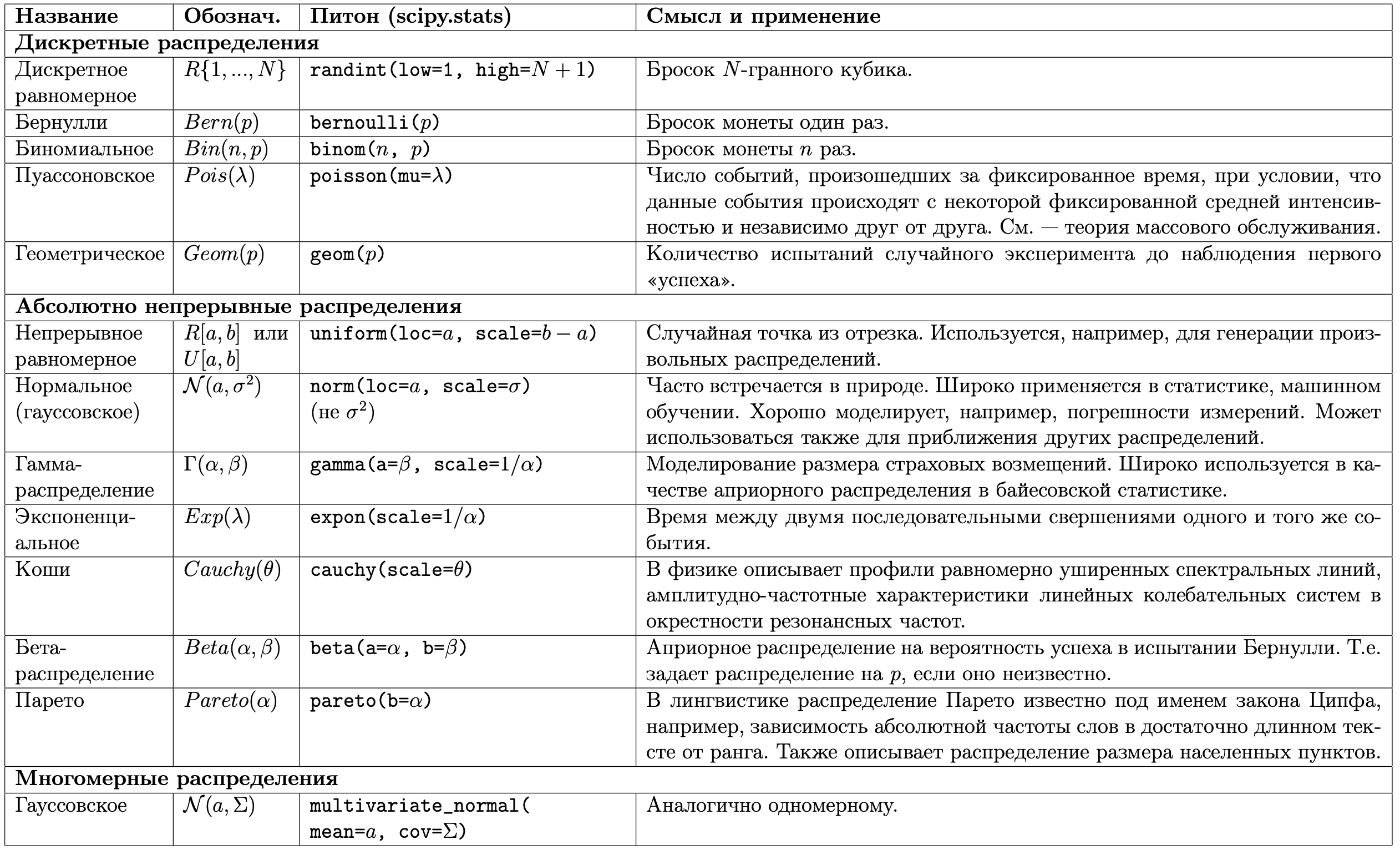
Problem set 1. Probability distribution. CDF and PDF.
Problem set 2. Random variables and random vectors.
Problem set 3. Independence. Convolution Formula.
Problem set 4. Expected value and variance.
Problem set 5. Convergence of random variables.
Problem set 6. Characteristic functions.
Problem set 7. Limit theorems.
Problem set 8. Gaussian vectors.
Lecture Notes
- Lecture 1 [02/09/22] [download]
- Lecture 2 [09/09/22] [download]
- Lecture 3 [16/09/22] [download]
- Lecture 4 [23/09/22] [download]
- Lecture 5 [30/09/22] [download]
- Lecture 6 [07/10/22] [download]
- Lecture 7 [14/10/22] [download]
- Lecture 8 [21/10/22] [download]
- Lecture 9 [28/10/22] [download]
- Lecture 10 [11/11/22] [download]
- Lectures 11 [18/11/22] [download]
- Lecture 12 [25/11/22] [download]
- Lecture 13 [02/12/22] [download]
Attendance & Marks
Course guidelines and grading system
At the end of this course, you will get a grade from 1 to 10 (you need at least 3 to pass) according to the following parameters:
- Max of 1 point for class attendance (1 if you missed no more than 2. And o,5 if you missed no more than 3)
- Max of 3 points for Test 1 [± 21.10]
- Max of 3 points for Test 2 [± 09.12]
- Max of 4 points for final exam on theory [16.12]
IMPORTANT: You must pass the exam on theory in order to pass the course.
Test 1 and 2 are closed-book, that is, you are not allowed to use any material. On the other hand, at the the theoretical exam, while preparing your solutions (and only at this moment), you are permitted to use any written material (lecture and seminar notes, printed notes or books) but not electronic devices (phones, laptops). In both cases, it is not permitted to help in any way to your classmates.
The number of points you get for each activity, is either an integer x or x+0.5.
If your final grade (after the final exam) is not an integer (z+0,5), you can solve an extra problem to raise your grade to z+1. Otherwise you get just z.
Every week, after class, I will upload a new homework. Each of you have to solve (or at least try to solve) these problems. I will randomly choose one of you during to seminar so that you can explain to everyone your solution.
Syllabus
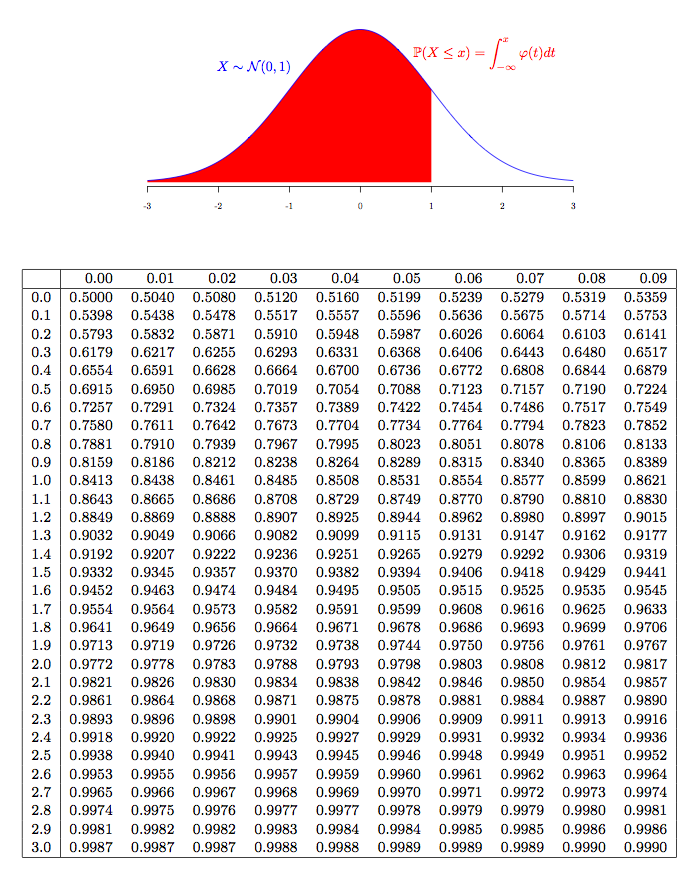
- Probability space. Properties of probability measure. Probability distribution. CDF and properties. Examples (discrete). Absolutely continuous distributions. PDF. Examples. Uniform, exponential, normal.
- Distributions in Rn. CDF and Properties. Independence and marginal distributions. PDF in Rn and Properties.
- Random elements. Random vector as a vector of random variables. Independence of random vectors.
- Criteria of Independence. Fubini’s theorem. Convolution formula.
- Expected value in general. Properties. Examples. Change variable theorem. Variance and examples. Jensen inequality.
- Conditional expectation. Properties.
- Conditional distribution.
- Convergence of random variables. Connection between different types of convergence. Examples where they doesn’t hold.
- Criteria of convergence. Borel-Cantelli lemma.
- Law of the iterated logarithm. SLLN 1. SLLN 2.
- Characteristic functions. CLT.
- Gaussian vectors.
Recommended literature
- Probability (Graduate Texts in Mathematics) 2nd Edition - Albert N. Shiryaev.
- Introduction to probability for Data Science - Stanley H. Shan. [download]
- Probability and Statistics for Data Science - Carlos Fernandez-Granda.
- Introduction To Probability - Joseph K. Blitzstein, Jessica Hwang.
- Мера и интеграл, Дьяченко М.И.
- Курс теории вероятностей и математической статистики, Севастьянов Б.A.
- Курс теории вероятностей, Чистяков В.П.
Recommended extra material
- Short lectures on measure theory: [playlist]
- Short lectures on Probability Theory [playlist]
- Probability theory course IMPA [playlist]
- Probability theory course Harvard University [playlist]
- Interactive videos on probability from 3Blue1Brown [video]
- Lectures in introduction to probability (in russian) [playlist]
- [link]